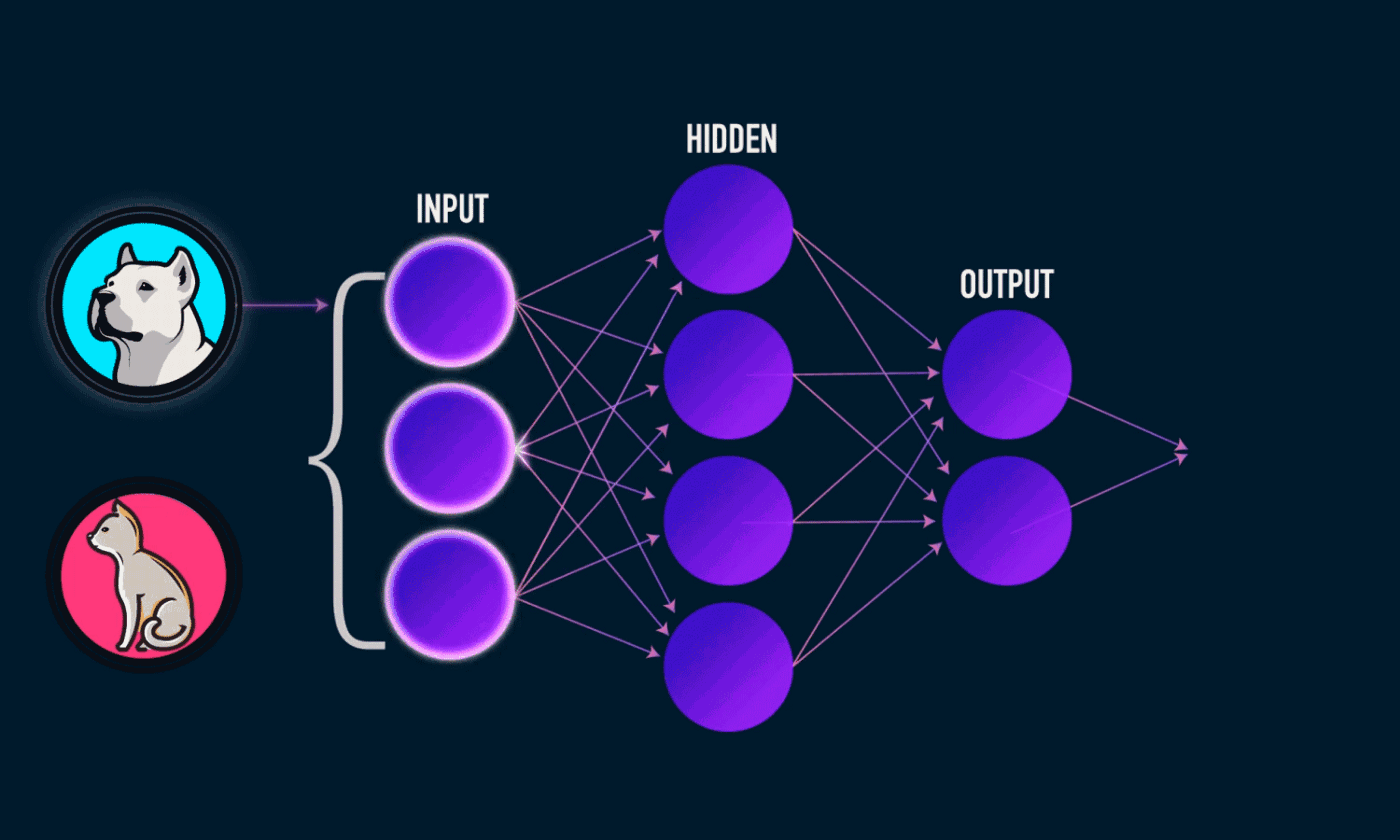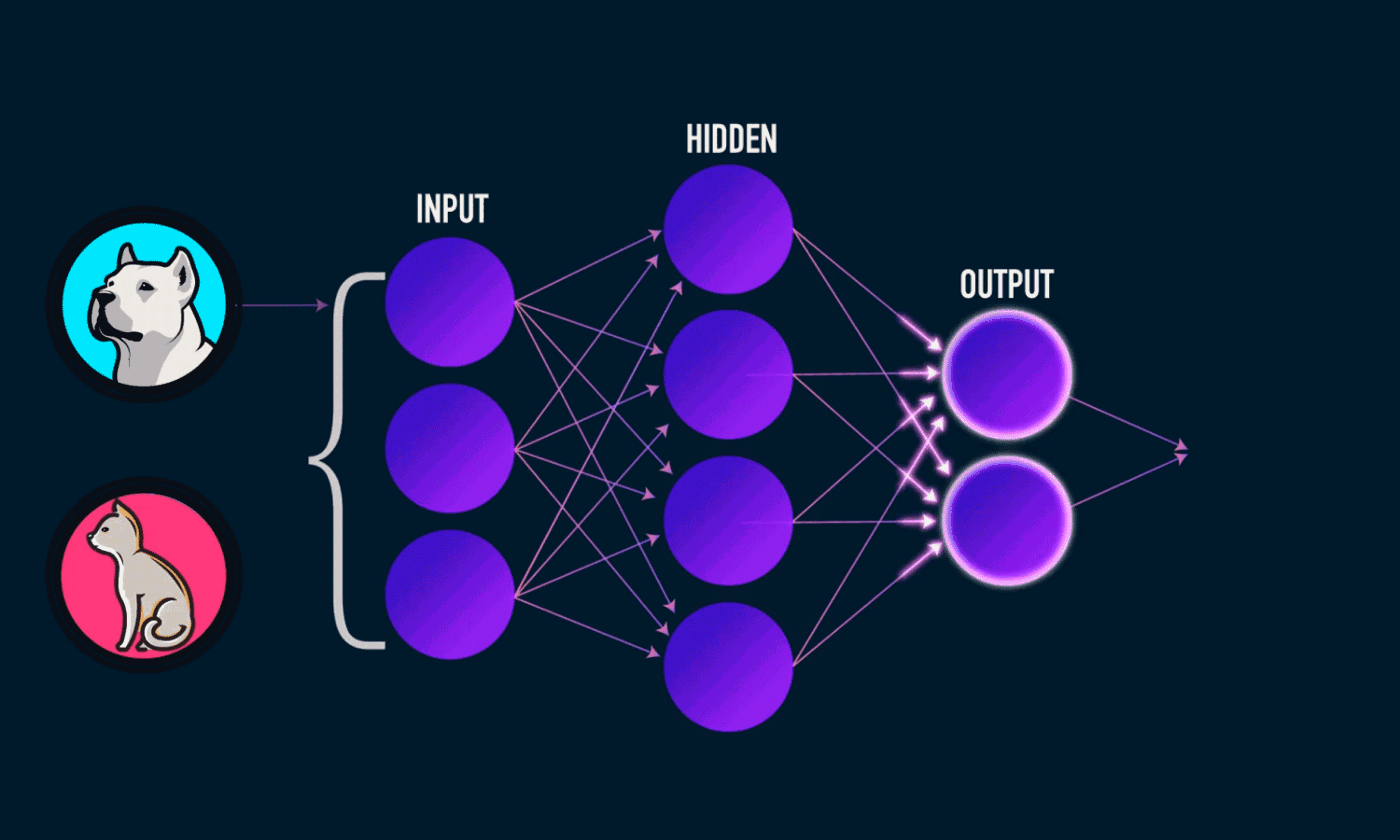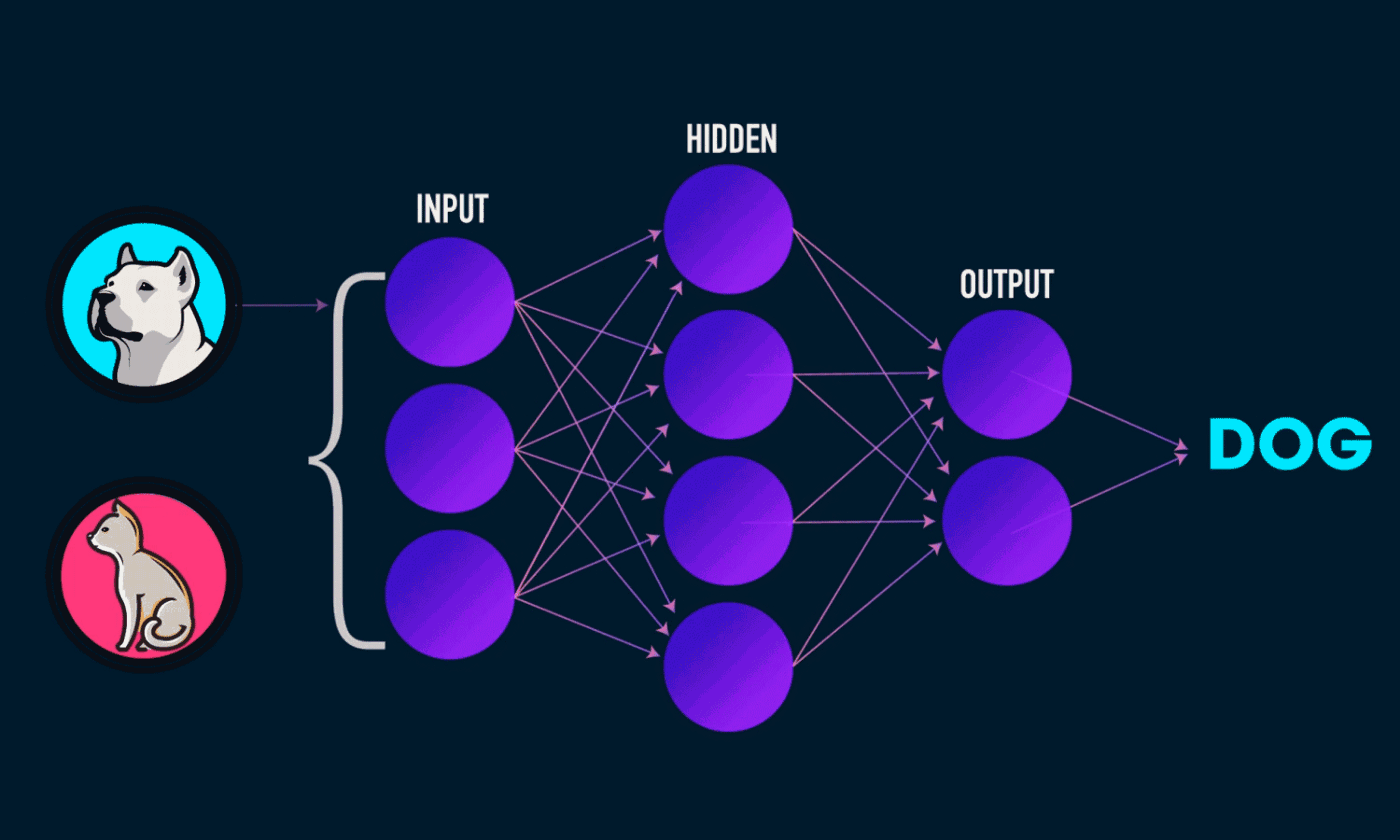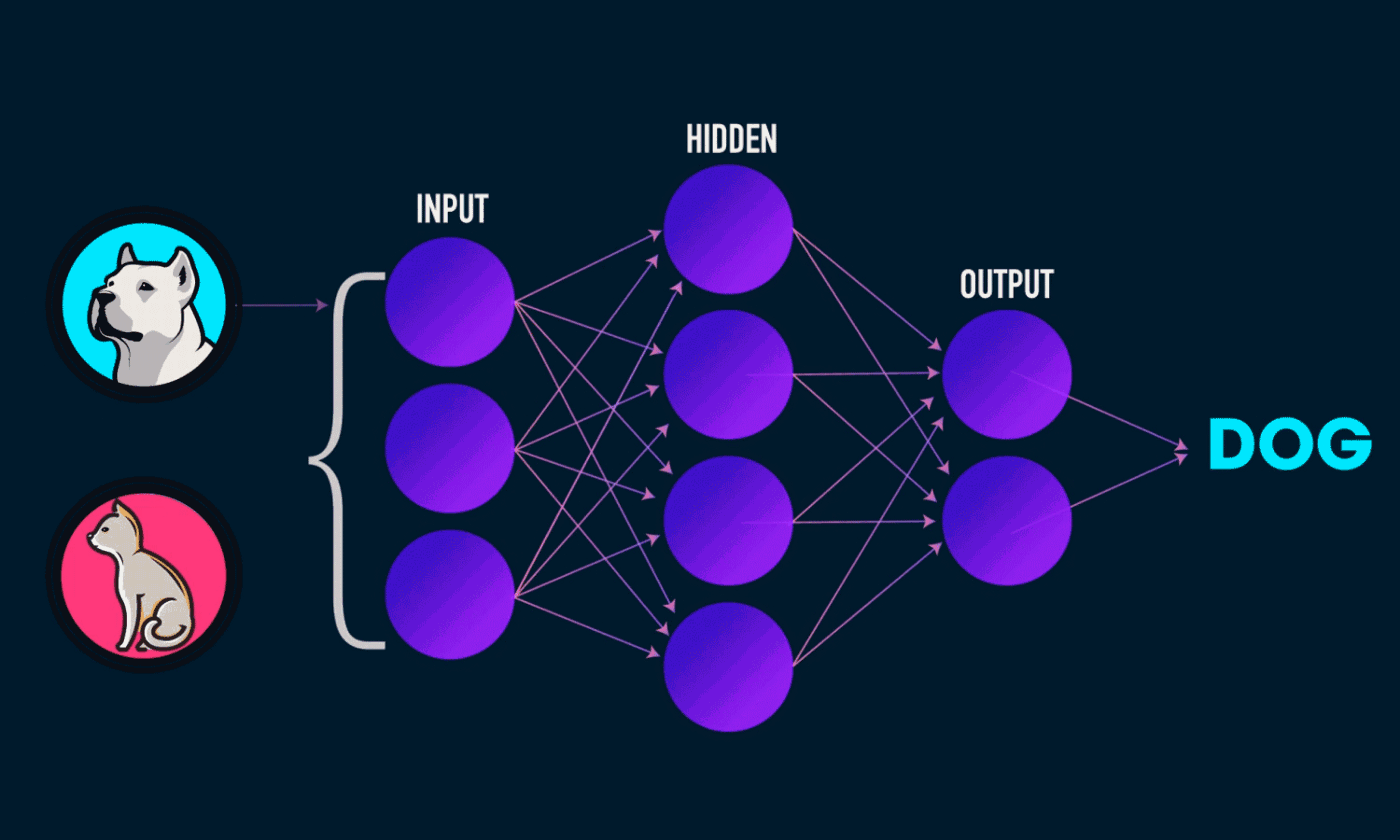
Text classification: algorithm vs neural networks

Text classification is the task of assigning predefined categories to free text. Documents, tweets, instagram feeds, email, basically anything that contains text. This has many interesting applications in the real world. One example
that you might be enjoying on a day to day basis is spam detection for your email. Or your news feed that is organized by topic. An example that might be more interesting to companies is sentiment analysis. How do my customers feel about my company?

Doing text classification with a neural network sounds pretty cool, but
can be pretty daunting. After all, neural networks are like black boxes,
or even black magic: you don’t really know what is happening, or how the
result was achieved. Before you even get to use the black box, you need to build it. What do you put in it? How many hidden layers? What kind of heuristics do we put in? What are the outputs? All these things are pretty complicated, especially if you’re just starting with Natural Language Processing (NLP), like I am 🤖.

Then, you need to train the model. How do you know if the model is properly trained? Or if the data you feed it is correct? After all, you want to work with text, but the neural networks are usually huge matrices of magic numbers. So arcane and complicated!

This is why sometimes you want to use a good old algorithm to do these sorts of things. Especially naive ones, because we can understand them. A classic algorithm to use is Multinomial Naive Bayes. This algorithm is naive because it assumes independence of features. This means that it does not care about the position of a word within a sentence, nor does it care about possible relations between the words.

For example, let’s take: “Cats are good pets, for they are clean and are not noisy”. In naive bayes, there is no relation between the words Cats, pets, clean and noisy. In NLP, this collection of words is called a bag of words. While this approach may seem naive, remember that we are not trying to understand the meaning of a sentence, but instead we are merely trying to find a proper classification.

Training the algorithm

In order to write an algorithm that classifies arbitrary text, we will need to create a data structure that has a bag of words per classification. We can then take text and see how that fits each of those bags of words.

We will need to provide some training data in order to build a bag of words for each classification. Let’s take a sentence from a fictional set of training data, and let’s give it the classification “amazing”.

Let’s break down the steps required to build a bag of words for “amazing”:

• Break down each sentence to a set of single words (tokenization).
• Filter out stop words
• Normalize the words by stemming them
• Convert to lower case to have case insensitive matching

The sentence we will work with is:

He told us a very exciting adventure story

First up, tokenizing. Tokenizing this sentence yields “He”, “told”, “us”, “a”, “very”, “exciting”, “adventure” and “story”. The result can vary depending on what tokenizer we use, since there are a ton of tokenizers out there, but generally speaking each word is taken individually.

Next, we filter out stop words, or very frequently used words. There is no definitive list of stop words, and it also depends on what goal we are processing text for, but for this article we will use the list defined here: http://xpo6.com/list-of-english-stop-words. After removing the stop words from our example sentence, we are left with: “told”, “exciting” “adventure”, “story”.

Finally, we should stem the words. This is needed so that the algorithm recognizes variations of the same word. For example, the stem of exciting is excit. This way, when we encounter words such as exciting, excitement, excite, etc. we can consider them a match. The resulting bag of words for the “amazing” category results in: “told”, “excit”, “adventur”, “stori”. Just like with tokenizers, there are many different stemmers out there, including different stemmers for different languages. A famous one is the Porter stemmer.

Then, we can move on to the next sentence and do the same thing for it’s classification. Create a new bag of words if it’s a new classification we haven’t trained yet, or if we have encountered the classification before, add new words to the bag until we are done.

Using the algorithm

Now that we have a bunch of classifications that each have a bags of words, we can leverage that to classify new sentences. We will need to prepare the sentence in the same way as we did the training data: Tokenize the sentence, filter out the stop words, and stem the words. Then, go through each word and check for each classification if it’s bag of words contains the word. If it does, you can increase the score for that classification. The classification that ultimately has the highest score is most likely to be the correct one. 👌

In pseudocode, this could look something like so:

def calcalateScore(sentence, classification) {
  score = 0;// go through each word in the sentence
  tokenize(sentence).each(word => {// skip stop words
    if (!stopWord(word)) {if (bagsOfWords[classification] contains stem(word)) {
        score += 1;
      }
    }
  }return score;
}

However, simply counting occurrences of words within individual bags might not be the best approach, since some words might occur in all bags, while other words might only occur in one or two, depending on the size of your training data. This means that categories with very large bags of words are almost guaranteed to get a high score, which may not always be a relevant match.

One way to solve this is to account for commonality of each word: words that we have seen many times in our training data yield less of a score then words we’ve only seen once or twice. So, instead of incrementing the score by 1 for each match, we can do a weighted increment:

score += 1 / numberOfOccurences(word);

This way, we should get better results. 😊

Conclusion

Using a machine learning algorithm without deep learning may feel a bit naive to do text classification, but one of the main advantages i feel it has over neural networks is that it’s a whole lot easier to explain as to why the algorithm came to a certain classification. And in the end, if results need to be interpreted by humans (such as the user!), being able to reason and explain as to why a certain classification was derived is a lot better then to say:

Because the neural network said so.📖